Mathematical Statistics

Normal Distribution

若随机变量 $X$ 服从一个位置参数为 $\mu$, 尺度参数为 $\sigma$ 的概率分布, 且其概率密度函数 (Probability Density Function, PDF) 为:

$$\begin{equation} f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \end{equation}$$

则这个随机变量称为正态随机变量, 正态随机变量服从的分布称为正态分布, 记作 $X \sim N(\mu,\sigma^2)$, 读作 $X$ 服从 $N(\mu,\sigma^2)$ (正态分布). 其中 $\mu$ 为均值 (数学期望 Mean), $\sigma$ 为标准差 (Standard Deviation).

正态分布 (又称 Gaussian Distribution) 是一种连续概率分布. 当 $\mu$ 为 0, $\sigma$ 为 1 时, 称为标准正态分布 (Standard Normal Distribution).

Central Limit Theorem

在自然界与生产中, 一些现象受到许多相互独立的随机因素的影响, 如果每个因素所产生的影响都很微小时, 总影响 (Sum) 可以看作服从正态分布.

相互独立的正态分布, 其和也是正态分布. 总体正态分布的均值等于各个分布的均值之和, $E(X_1+\dots+X_n)=E(X_1)+\dots+E(X_n)=n\mu$. 假设协方差为 0, 则总体正态分布的方差等于各个分布的方差之和, ${Var(X_1+\dots+X_n)}={Var(X_1)+\dots+Var(X_n)}={n}\sigma^2$, 可以得到总体正态分布的标准差为 $\sqrt{n}\sigma$.

设随机变量 $X_1,X_2,\dots,X_n$ 独立同分布(Independent Identically Distribution), 且均值为 $E(X_i)=\mu$, 方差为 $D(X_i)=\sigma^2$, 对于任意 $x$, 其分布函数为

$$F_n(x)=P\left\{\frac{\sum_{i=1}^n{X_i}-n\mu}{\sqrt{n}\sigma}\leq{x}\right\}$$

满足

$$\begin{equation} \lim_{n\to\infty}F_n(x) =\lim_{n\to\infty}P\left\{\frac{\sum_{i=1}^n{X_i}-n\mu}{\sqrt{n}\sigma}\leq{x}\right\} =\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x{e^{-\frac{t^2}{2}}dt} =\varnothing(x) \end{equation}$$

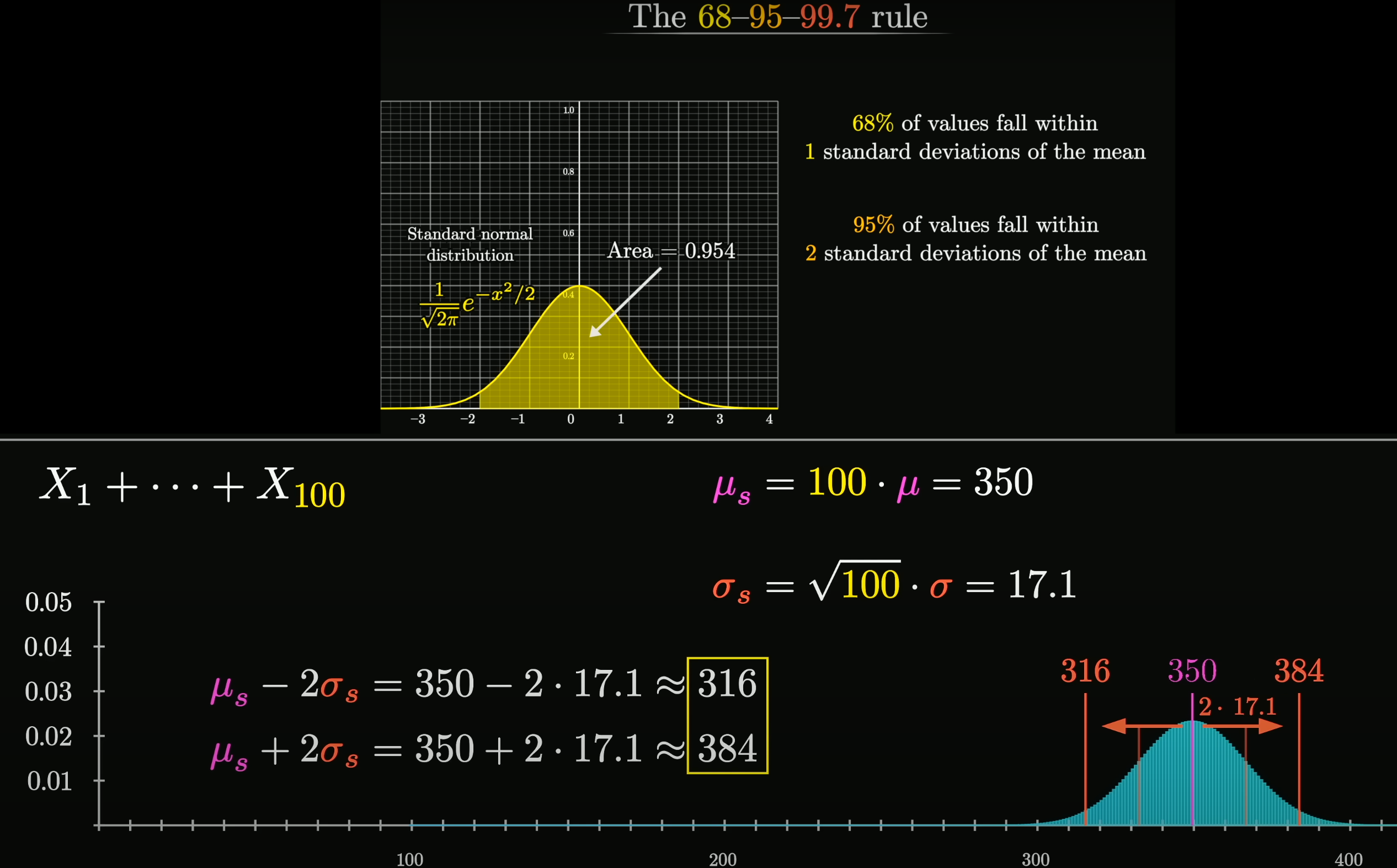
独立同分布的中心极限定理说明, 当 $n$ 足够大时, 随机变量 $X_n=\sum\limits_{i=1}^n{X_i}$ 近似服从正态分布 $N(n\mu,n\sigma^2)$; 标准化后的随机变量 $Y_n=\frac{\sum_{i=1}^n{X_i}-n\mu}{\sqrt{n}\sigma}$ 近似服从标准正态分布 $N(0,1)$.

更一般化的中心极限定理, 可参见林德伯格中心极限定理 (Lindeberg CLT) etc.

Gaussian Integral

$$\begin{equation} \int_{-\infty}^{\infty}e^{-x^2}dx=\sqrt{\pi} \end{equation}$$

高维空间求解高斯积分:

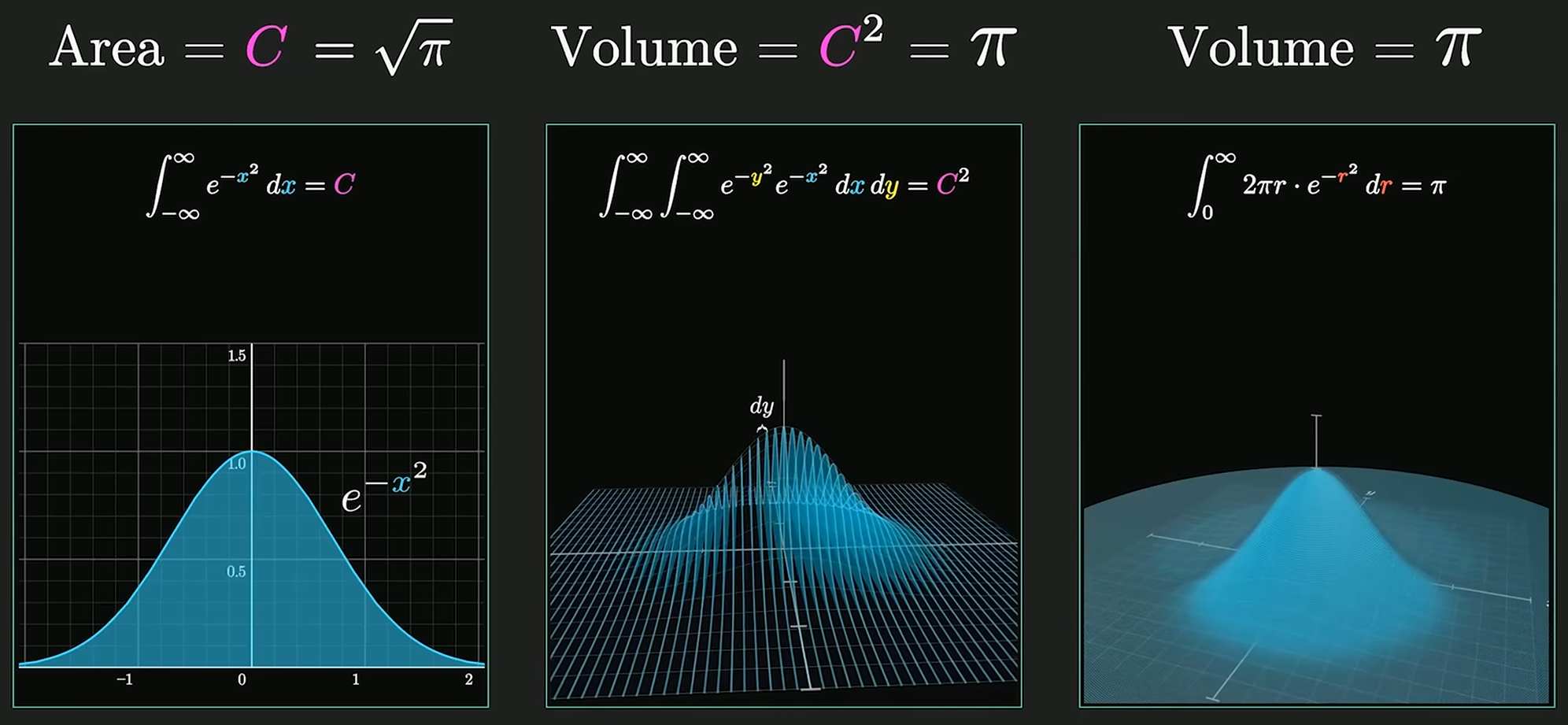
对于正态分布, 系数 $\frac{1}{\sqrt{\pi}}$ 使得概率密度函数的积分为 1, 即 $\int_{-\infty}^{\infty}f(x)dx=1$, 使其成为有意义的概率分布.

Binomial Distribution

重复 n 次独立的伯努利试验, $X \sim B(n,p)$, 期望值 $E(X)=np$, 方差 $D(X)=np(1-p)$:

$$\begin{equation} P(X=k)=C_n^kp^k(1-p)^{n-k} \end{equation}$$

Bayes Theorem

Bayes theorem:

$$P(A \cap B)=P(A|B)P(B)=P(B|A)P(A)\Rightarrow$$ $$\begin{equation} P(A|B)=\frac{P(B|A)P(A)}{P(B)}=\frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg{A})P(\neg{A})} \end{equation}$$

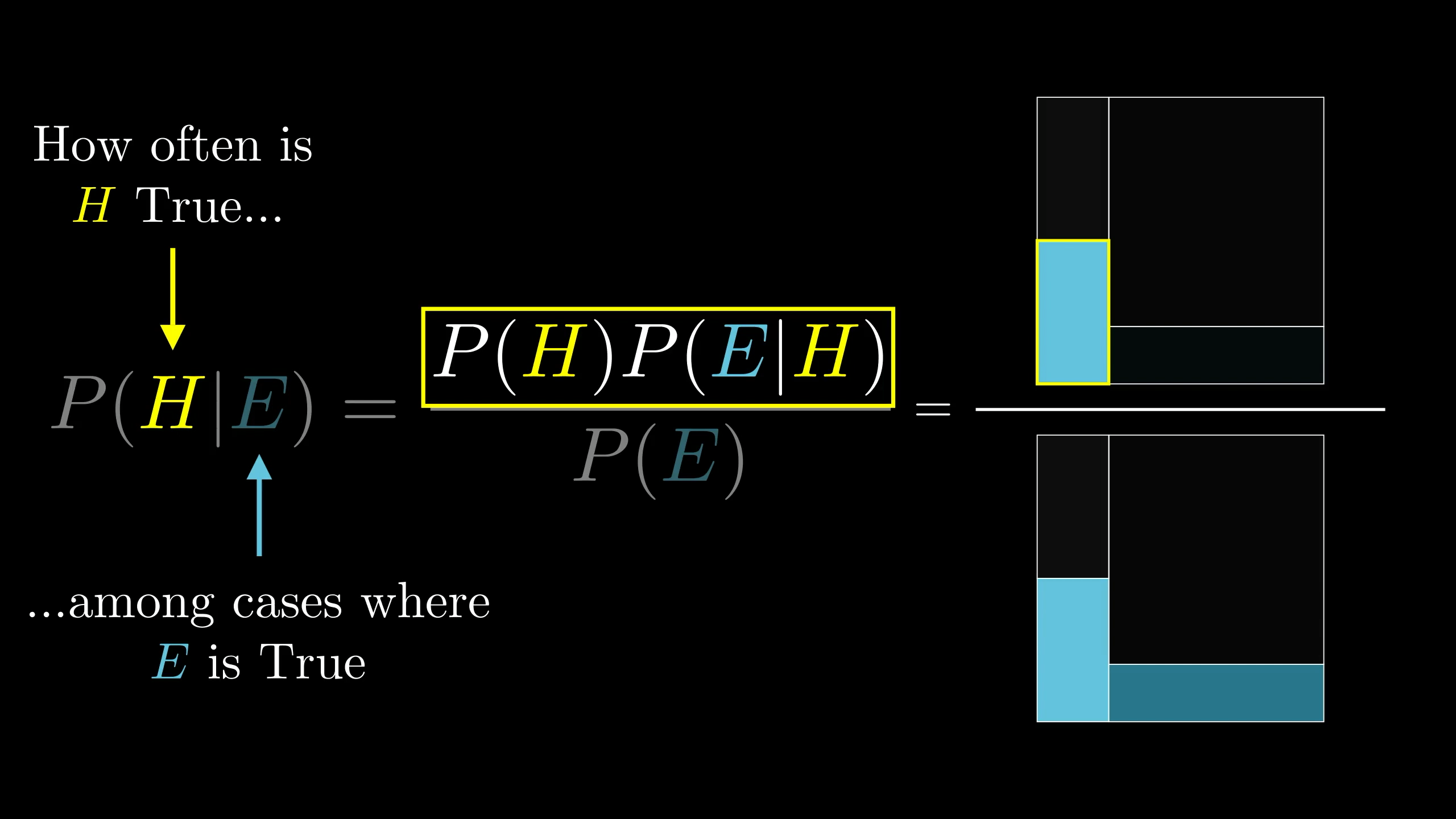
其中, $\frac{P(B|A)}{P(B|\neg{A})}$ 称为贝叶斯系数 (Bayes Factor):

$$O(A|B)=\frac{P(A|B)}{P(\neg{A}|B)}=\frac{P(A|B)P(B)}{P(\neg{A}|B)P(B)}=\frac{P(B|A)P(A)}{P(B|\neg{A})P(\neg{A})}=O(A)\frac{P(B|A)}{P(B|\neg{A})}$$

Information Entropy

信息熵 是对信息量的度量 ($E[I]$), 概率小的事件发生所带来的信息量大, 概率大的事件发生所带来的信息量小, 即概率小, 出现机会小, 不确定性大, 信息熵大, 信息量大:

$$\begin{equation} H(X)=E[-\log_2{P(x_i)}]=-\sum\limits_{i=1}^n{P(x_i)\log_2{P(x_i)}} \end{equation}$$