Multilayer Perceptron

多层感知机是一种前馈神经网络 (Feedforward Neural Network) 就像是一个模拟大脑处理信息的过程, 通过多层处理 (输入层, 隐藏层, 输出层), 从原始数据中提取特征, 并做出预测或分类, 它通过调整内部连接权重来学习和改进其预测能力.

Linear Mapping

线性变换 $H^l=W^lX^{l-1}+B^l$:

• $w_{ij}^l$ (weight): 第 $l$ 层第 $i$ 个节点与上一层第 $j$ 个节点连接的权重.
• $b_i^l$ (bias): 第 $l$ 层第 $i$ 个节点的偏置.

$$H=\begin{bmatrix} w_{00}^l & w_{01}^l & \dots & w_{0n}^l \\ w_{10}^l & w_{11}^l & \dots & w_{1n}^l \\ \vdots & \vdots & \ddots & \vdots \\ w_{k0}^l & w_{k1}^l & \dots & w_{kn}^l \end{bmatrix} \begin{bmatrix} x_0^{l-1} \\ x_1^{l-1} \\ \vdots \\ x_n^{l-1} \end{bmatrix} +\begin{bmatrix} b_0^l \\ b_1^l \\ \vdots \\ b_k^l \end{bmatrix}$$

Activation Function

激活函数 $y=\sigma(H)$, $X^l=\sigma(H^l)$:

• 引入非线性特性, 使得网络可以学习和拟合复杂函数.
• ReLU (Rectified Linear Unit, 线性整流单元): $\sigma(H)=\max(0,H)$, 可以解决梯度消失问题 (越靠近输入层的神经元梯度越接近 0), 加速收敛.
• Sigmoid: $\sigma(H)=\frac{1}{1+e^{-H}}$.
• e.g. 归一化函数, 使得输出值在 0 到 1 之间, 可以使得整个网络成为概率模型.

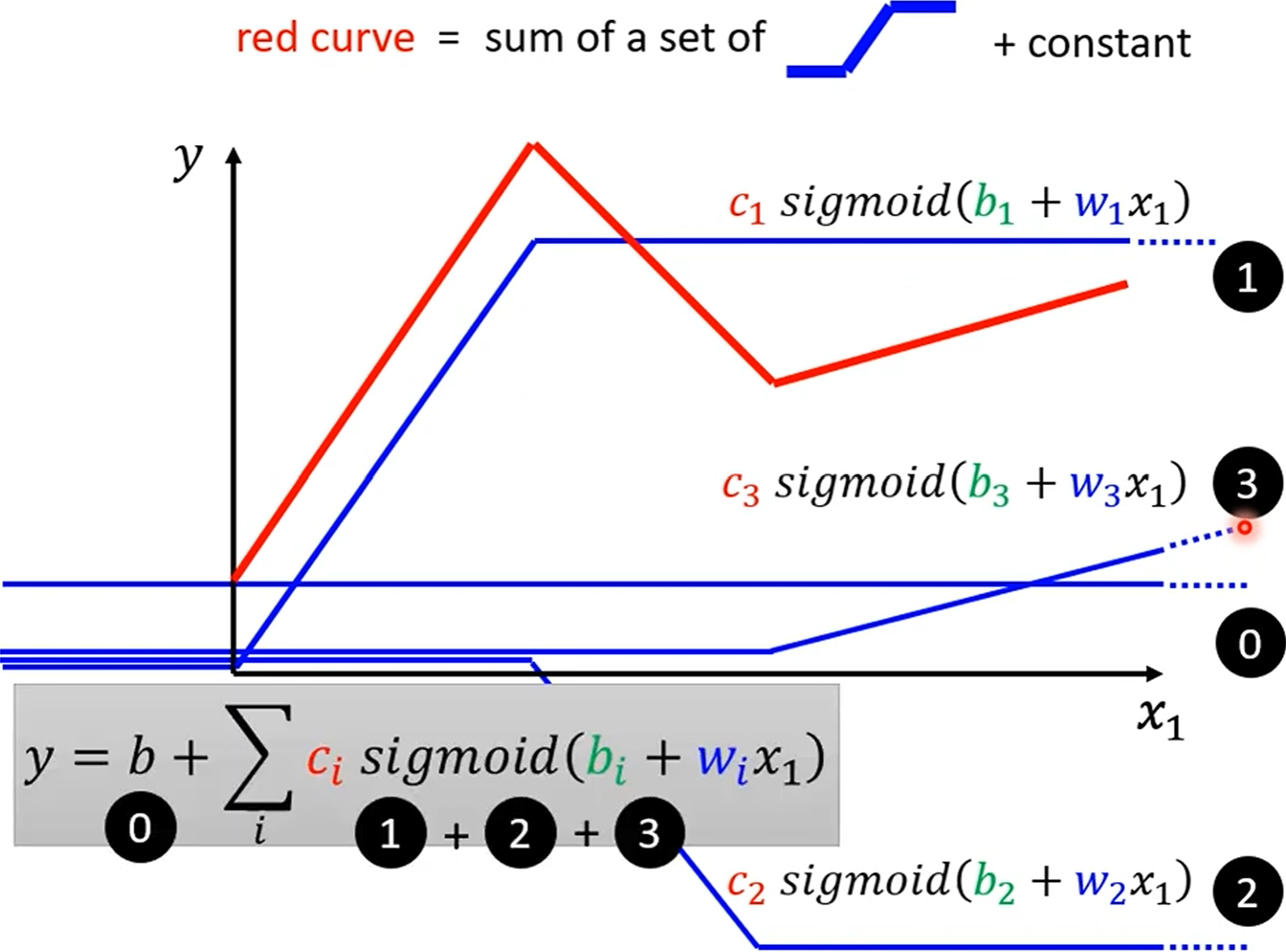
Loss Function

损失函数 $L(y,\hat{y})$:

• 用于衡量真实值(或人工标注值) $y$ 与模型预测值 $\hat{y}$ 之间的差异.
• 常见的损失函数有均方误差 (Mean Squared Error, MSE) 和交叉熵 (Cross Entropy).
  • 均方误差: $L(y,\hat{y})=\frac{1}{n}\sum\limits_{i=1}^n(y_i-\hat{y}_i)^2$.
  • 交叉熵: $L(y,\hat{y})=-\sum\limits_{i=1}^n{y_i\log(\hat{y}_i)}$, 常用于 classification 任务.
  • Selective synaptic plasticity: $L'(\theta)=L(\theta)+\lambda\sum\limits_ib_i(\theta_i'-\theta_i)^2$.

Deep

$|\mathcal{H}|$ is the size of hypothesis space, larger $|\mathcal{H}|$ means deeper model:

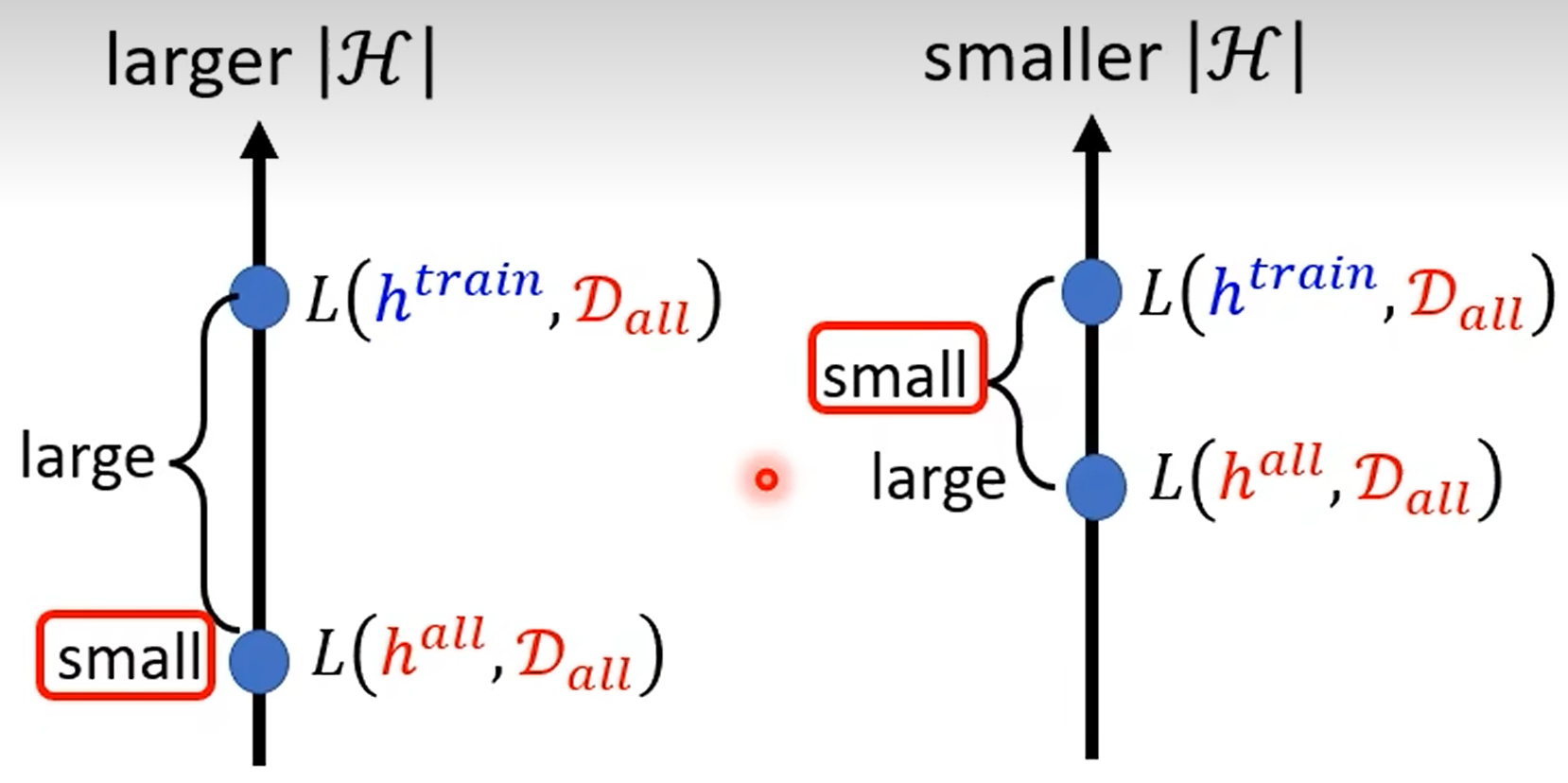
Deep model need less neurons (parameters) to represent same function, means deep model has smaller $|\mathcal{H}|$, flat/shallow model has larger $|\mathcal{H}|$.

Learning

Learning is the process of minimizing loss function, finally find out the right weights and biases:

• Early stopping.
• Dropout.
• Regularization.
• New activation function.
• Adaptive learning rate.

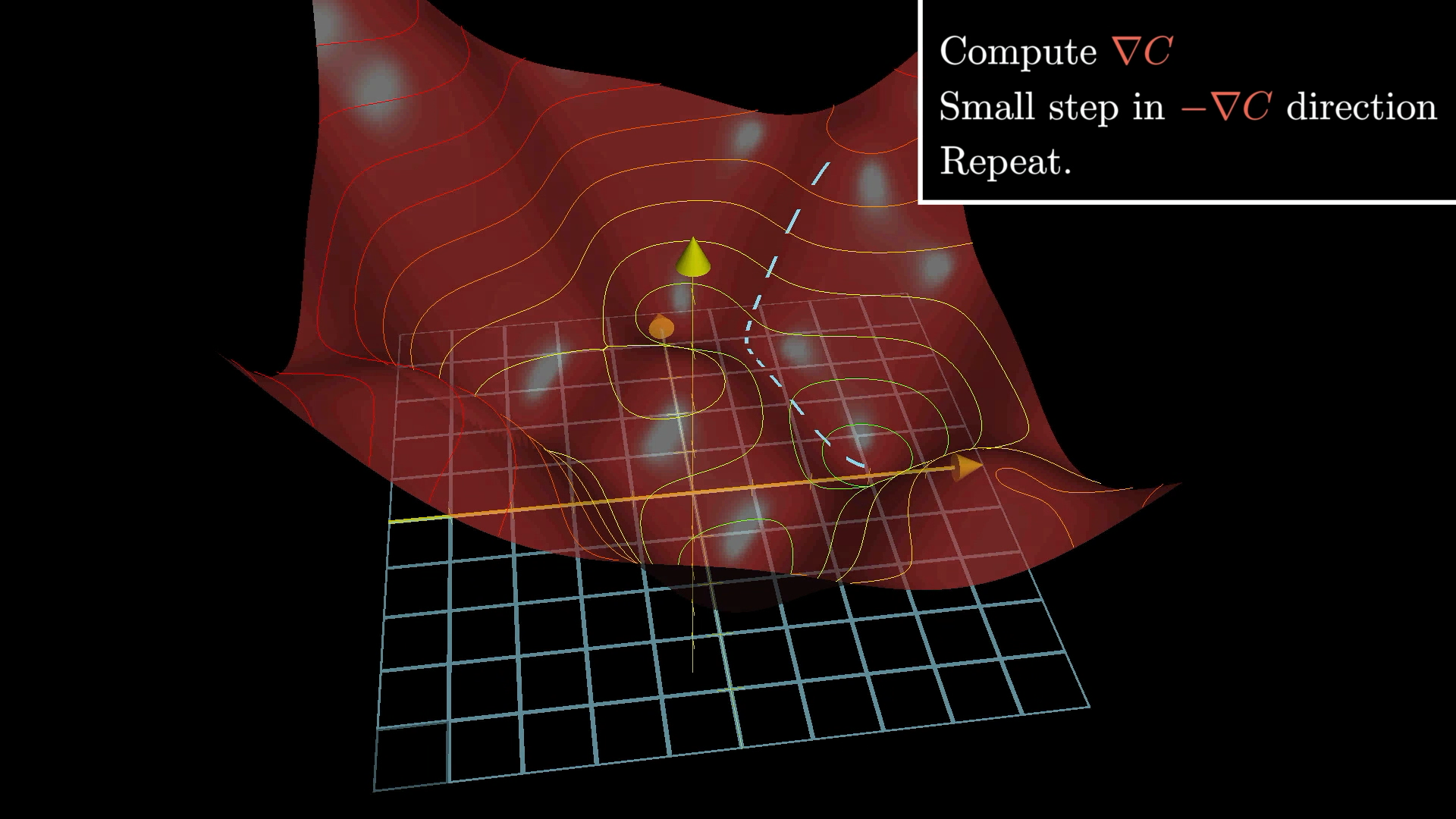
Gradient Descent

通过梯度下降算法, 优化损失函数, 使其最小化 (沿梯度下降方向, 调整 W 和 B):

$$\begin{equation} \theta_{t+1}=\theta_t-\eta\nabla{L} \end{equation}$$

其中, $\eta$ 为学习率, $L$ 为损失函数, $\nabla{L}$ 为损失函数的梯度, $\theta$ 为模型参数, $t$ 为迭代次数.

$$\begin{split} \arg\min{L(\theta)}&=L(a,b)+\frac{\partial{L(a,b)}}{\partial{\theta_1}}(\theta_1-a)+\frac{\partial{L(a,b)}}{\partial{\theta_2}}(\theta_2-b)\\ &+\dots+\frac{1}{n!}\frac{\partial^n{L(a,b)}}{\partial{\theta_1^n}}(\theta_1-a)^n+\frac{1}{n!}\frac{\partial^n{L(a,b)}}{\partial{\theta_2^n}}(\theta_2-b)^n\\ &\approx{L(a,b)}+\frac{\partial{L(a,b)}}{\partial{\theta_1}}(\theta_1-a)+\frac{\partial{L(a,b)}}{\partial{\theta_2}}(\theta_2-b) \\ &\Rightarrow \begin{bmatrix}\theta_1-a\\\theta_2-b\end{bmatrix} =-\eta\begin{bmatrix}\frac{\partial{L(a,b)}}{\partial{\theta_1}}\\\frac{\partial{L(a,b)}}{\partial{\theta_2}}\end{bmatrix} \\ &\Rightarrow \begin{bmatrix}\theta_1 \\ \theta_2\end{bmatrix} =\begin{bmatrix}a\\b\end{bmatrix}-\eta\begin{bmatrix}\frac{\partial{L(a,b)}}{\partial{\theta_1}}\\\frac{\partial{L(a,b)}}{\partial{\theta_2}}\end{bmatrix} \end{split}$$

def convex_function(x):
    return x**2

def gradient_descent(initial_x, learning_rate, num_iterations):
    x_values = [initial_x]
    y_values = [convex_function(initial_x)]

    x = initial_x

    for i in range(num_iterations):
        gradient = 2 * x  # 函数 f(x) = x^2 的导数为 f'(x) = 2x
        x -= learning_rate * gradient

        x_values.append(x)
        y_values.append(convex_function(x))

    return x_values, y_values

Gradient

一个优秀的梯度下降算法, 需要满足以下几个条件:

• 高效性: 梯度下降算法的迭代次数尽可能少. 当距离最小值较远时, $\nabla{L}\gg0$, 当距离最小值较近时, $\nabla{L}\to0$, 这样的梯度下降算法可以更快地收敛. 反之, 当距离最小值较远时, $\nabla{L}\to0$, 这样的梯度下降算法更慢收敛.
• 稳定性: 梯度下降算法的迭代过程尽可能稳定. Maxout 激活函数拟合能力非常强, 可以拟合任意的凸函数.
• 鲁棒性: 梯度下降算法对于初始值的选择或者特定的线索片段不敏感. Dropout 策略 减少神经元之间复杂的共适应关系 (每个神经元有 $p\%$ 概率不被激活), 迫使网络去学习更加鲁棒的特征, 缓解过拟合问题, 提高模型的泛化能力.

Learning Rate

必要时需要调整学习率, 使得梯度下降更快收敛:

• 如果学习率过大, 可能会导致梯度下降不稳定, 甚至发散.
• 如果学习率过小, 可能会导致梯度下降收敛速度过慢.

常见的学习率调整策略有:

• Learning rate decay:
  • 阶梯衰减 (Step Decay): $\eta_t=\frac{\eta}{\sqrt{t+1}}$.
  • 线性衰减 (Linear Decay): $\eta_t=\eta(1-\frac{t}{T})$.
  • 指数衰减 (Exponential Decay): $\eta_t=\eta{e^{-kt}}$.
  • 余弦衰减 (Cosine Decay): $\eta_t=\eta\frac{1+\cos(\frac{\pi{t}}{T})}{2}$.
• Warm up learning rate: increase and then decrease learning rate.
• SGD with momentum: $w_{t+1}=w_t+v_{t+1}=w_t+\lambda{v_t}-\eta{g_t}$.
• Adaptive learning rate:
  • AdaGrad: adaptive sub-gradient method, $w_{t+1}=w_t-\frac{\frac{\eta}{\sqrt{t+1}}}{\sqrt{\frac{1}{t+1}\sum_{i=0}^t{g_i^2}}}g_t=w_t-\frac{\eta}{\sqrt{\sum_{i=0}^t{g_i^2}}}g_t$.
  • RMSprop: root mean square propagation, $w_{t+1}=w_t-\frac{\eta}{\sigma_t}g_t=w_t-\frac{\eta}{\sqrt{\alpha\sigma_{t-1}^2}+(1-\alpha)g_t^2}g_t$,
  • Adam: adaptive moment estimation (Momentum + RMSprop).
  • RAdam: start with SGDM, then switch to Adam.

Critical Point

当遇到 $\nabla{L}=0$ 的情况时, 可能是以下几种情况:

• 局部最小值 (Local Minimum).
• 局部最大值 (Local Maximum).
• 鞍点 (Saddle Point).

此时利用泰勒级数展开, 可以得到:

$$\begin{split} L(\theta)&\approx{L(\theta_0)}+\nabla{L(\theta_0)}(\theta-\theta_0)+\frac{1}{2}(\theta-\theta_0)^T\nabla^2{L(\theta_0)}(\theta-\theta_0)\\ &=L(\theta_0)+\frac{1}{2}(\theta-\theta_0)^T\nabla^2{L(\theta_0)}(\theta-\theta_0) \end{split}$$

其中, $\nabla^2{L(\theta_0)}$ 为 Hessian 矩阵, 为二阶导数矩阵:

• 当 $\nabla^2{L(\theta_0)}$ 为正定矩阵时, $\theta_0$ 为局部最小值.
• 当 $\nabla^2{L(\theta_0)}$ 为负定矩阵时, $\theta_0$ 为局部最大值.
• 当 $\nabla^2{L(\theta_0)}$ 为不定矩阵时, $\theta_0$ 为鞍点.

Saddle Point

在高维空间中, 鞍点的数量远远多于局部最小值. 深度神经网络拥有大量的参数, 使得其损失函数的鞍点数量远远多于局部最小值.

Backpropagation

反向传播算法: 从最小化损失函数出发, 由输出层到输入层, 通过链式法则, 计算每一层的梯度, 从而更新权重和偏置.

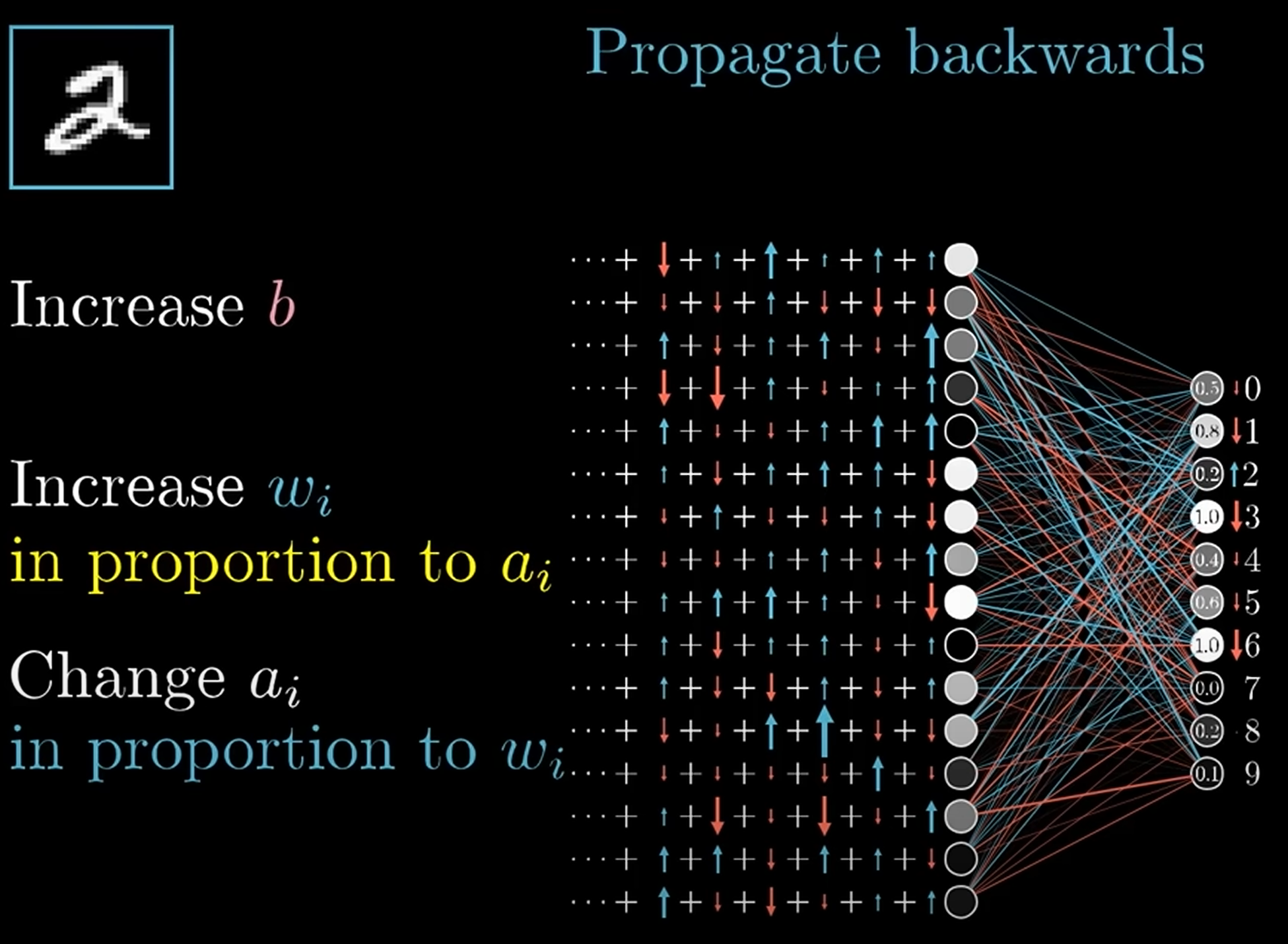
Derivative chain rule (链式法则):

$$\begin{split} \frac{\partial{L}}{\partial{w_{ij}^l}} &=\frac{\partial{L}}{\partial{x_i^l}}\cdot \frac{\partial{x_i^l}}{\partial{z_i^l}}\cdot \frac{\partial{z_i^l}}{\partial{w_{ij}^l}} \\ &=\frac{\partial{L}}{\partial{x_i^l}}\cdot \frac{\partial{\sigma(z_i^l)}}{\partial{z_i^l}}\cdot \frac{\partial(X^{l-1}W_i^l+b_i^l)}{\partial{w_{ij}^l}} \\ &=\delta_i^l\cdot\sigma'(z_i^l)\cdot{x_j^{l-1}} \\ \frac{\partial{L}}{\partial{b_i^l}} &=\frac{\partial{L}}{\partial{x_i^l}}\cdot \frac{\partial{x_i^l}}{\partial{z_i^l}}\cdot \frac{\partial{z_i^l}}{\partial{b_i^l}} \\ &=\frac{\partial{L}}{\partial{x_i^l}}\cdot \frac{\partial{\sigma(z_i^l)}}{\partial{z_i^l}}\cdot \frac{\partial(b_i^l+W_i^lX^{l-1})}{\partial{b_i^l}} \\ &=\delta_i^l\cdot\sigma'(z_i^l) \\ \frac{\partial{L}}{\partial{x_j^{l-1}}} &=\sum\limits_{i=0}^{N_l-1}\frac{\partial{L}}{\partial{x_i^l}}\cdot \frac{\partial{x_i^l}}{\partial{z_i^l}}\cdot \frac{\partial{z_i^l}}{\partial{x_j^{l-1}}} \\ &=\sum\limits_{i=0}^{N_l-1}\frac{\partial{L}}{\partial{x_i^l}}\cdot \frac{\partial{\sigma(z_i^l)}}{\partial{z_i^l}}\cdot \frac{\partial(W_i^lX^{l-1}+b_i^l)}{\partial{x_j^{l-1}}} \\ &=\sum\limits_{i=0}^{N_l-1}\delta_i^l\cdot\sigma'(z_i^l)\cdot{w_{ij}^l} \end{split}$$

outcomes

$$\begin{equation} \nabla{L}=\begin{bmatrix} \frac{\partial{L}}{\partial{w^1}} \\[0.8em] \frac{\partial{L}}{\partial{b^1}} \\[0.5em] \vdots \\[0.5em] \frac{\partial{L}}{\partial{w^l}} \\[0.8em] \frac{\partial{L}}{\partial{b^l}} \end{bmatrix} \end{equation}$$

Mini-Batch

Utilize parallel computing (GPU) to speed up training process:

• Divide training data into mini-batches.
• Update weights and biases for each mini-batch.
• Repeat until convergence.

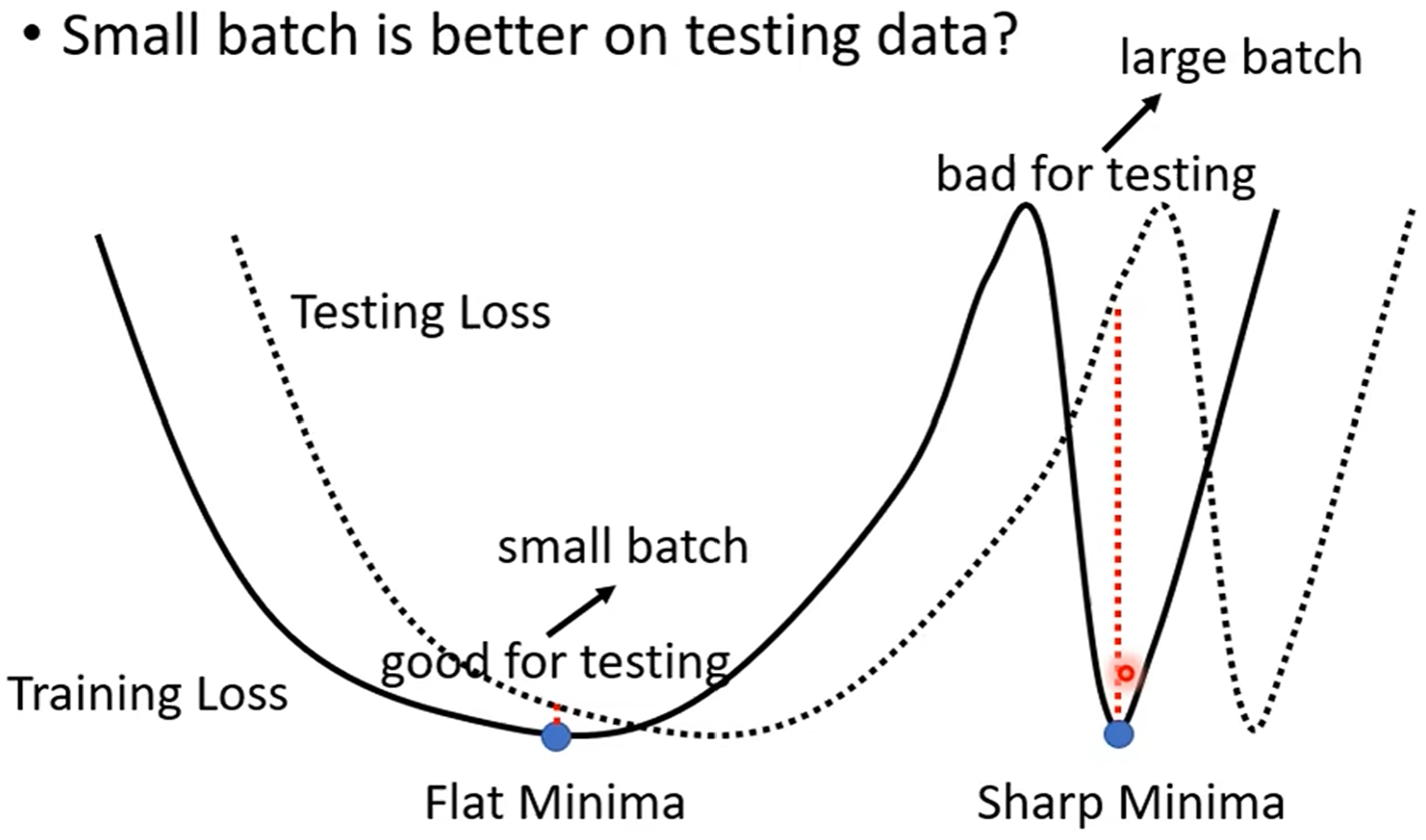
Batch Size	Small	Large
Speed (Sequential)	Faster	Slower
Speed (Parallel)	Same	Same
One Epoch Time	Slower	Faster
Gradient	Noisy	Stable
Optimization	Better	Worse
Generalization	Better	Worse

class Network(object):
    def SGD(self, training_data, epochs, mini_batch_size, eta, test_data=None):
        """Train the neural network using mini-batch stochastic
        gradient descent.  The ``training_data`` is a list of tuples
        ``(x, y)`` representing the training inputs and the desired
        outputs.  The other non-optional parameters are
        self-explanatory.  If ``test_data`` is provided then the
        network will be evaluated against the test data after each
        epoch, and partial progress printed out.  This is useful for
        tracking progress, but slows things down substantially."""
        if test_data:
            n_test = len(test_data)
        n = len(training_data)
        for j in range(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k : k + mini_batch_size]
                for k in range(0, n, mini_batch_size)
            ]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print(
                    "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)
                )
            else:
                print("Epoch {0} complete".format(j))

    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backpropagation(x, y)
            nabla_b = [nb + dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw + dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [
            w - (eta / len(mini_batch)) * nw for w, nw in zip(self.weights, nabla_w)
        ]
        self.biases = [
            b - (eta / len(mini_batch)) * nb for b, nb in zip(self.biases, nabla_b)
        ]

    def backpropagation(self, x, y):
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x]  # list to store all the activations, layer by layer
        zs = []  # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation) + b
            zs.append(z)
            activation = self.non_linearity(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * self.d_non_linearity(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in range(2, self.num_layers):
            z = zs[-l]
            sp = self.d_non_linearity(z)
            delta = np.dot(self.weights[-l + 1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l - 1].transpose())
        return (nabla_b, nabla_w)